正如现实世界在镜子中的像一样,赋范线性空间也有它的对偶空间,一个算子也有它的共轭算子,共轭的概念主要出自于代数,是一种对称性的刻画,为后面的理论研究有很大帮助。
第4章 共轭空间与共轭算子
共轭空间的基本概念以及表示定理
定义4.1
称$X^*$为$X$的共轭空间
注:从定义上来看,实际就是从X到数域K的有界线性算子全体
$L^p[a,b]$的共轭空间
$ f $ 是 $ L^{p}[a, b] $ 上的有界线性泛函, 则存在唯一的 $ y(t) \in L^{q}[a, b],\left(\frac{1}{p}+\right. \left.\frac{1}{q}=1\right) $, 使得
$f(x)=\int_{a}^{b} x(t) y(t) \mathrm{d} t, \forall x \in L^{p}[a, b],$$\text { 且 }\|f\|=\|y\|_{q}=\left(\int_{a}^{b}|y(t)|^{q} \mathrm{~d} t\right)^{\frac{1}{q}} \text {. }$
Rieze表示定理
设 $ H $ 是一个 Hilbert 空间, $ f$ 是 $ H$ 上定义的有界 线性泛函, 则存在唯一的 $ y_{f} \in H $, 使得
$f(x)=\left(x, y_{f}\right), \forall x \in H$
推论(Hilbert空间的共轭空间)
设 $ H $ 是一个 Hilbert 空间,则$H=H^*$. 此处的等号表示同构意义下的相等,不是集合相等
注:上面的几个定理实际给出了一类特殊的算子(泛函)的表示形式,比如有限维空间下的线性变换
可以用矩阵表示,如果映射到数域K上,那么这个矩阵实际就是一个向量,原本线性变换只是一个抽象
的符号,以及用映射的定义来表示,通过同构,可以用一个具体的空间中的元素来把线性变换表示出来
在无穷维线性空间中,泛函同样可以有一个具体的表示形式,泛函空间一样可以同构到一个具体的空间
共轭算子的提出
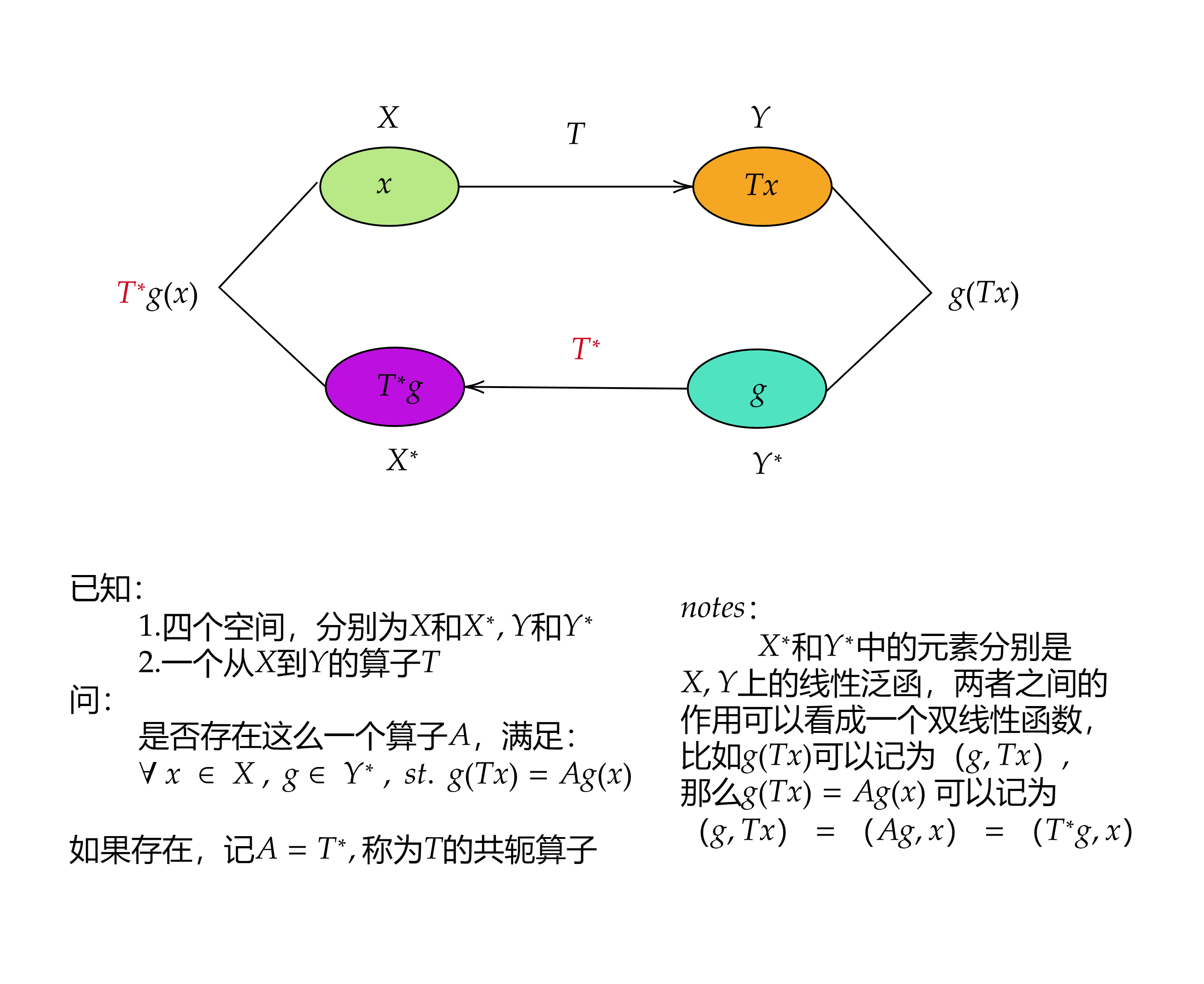
原始定义
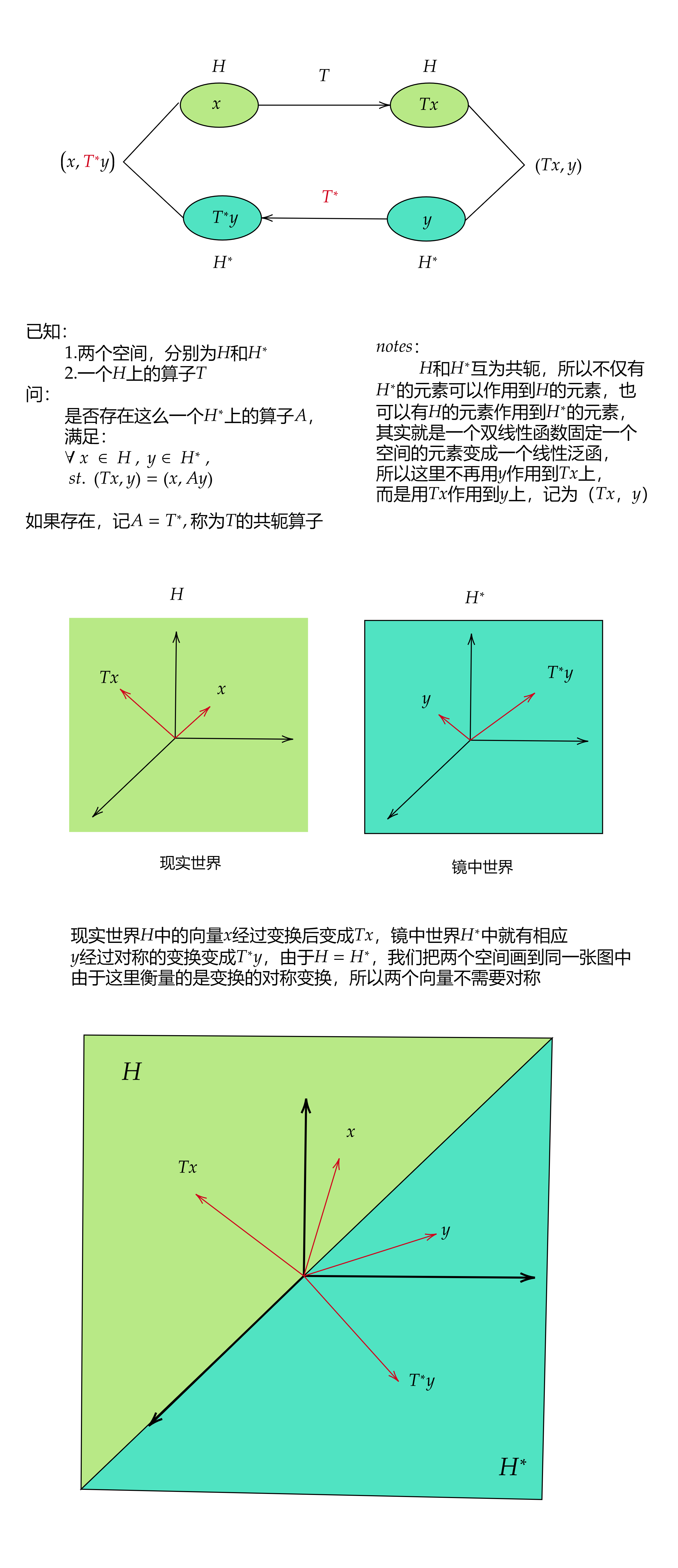
Hilbert空间上的共轭算子
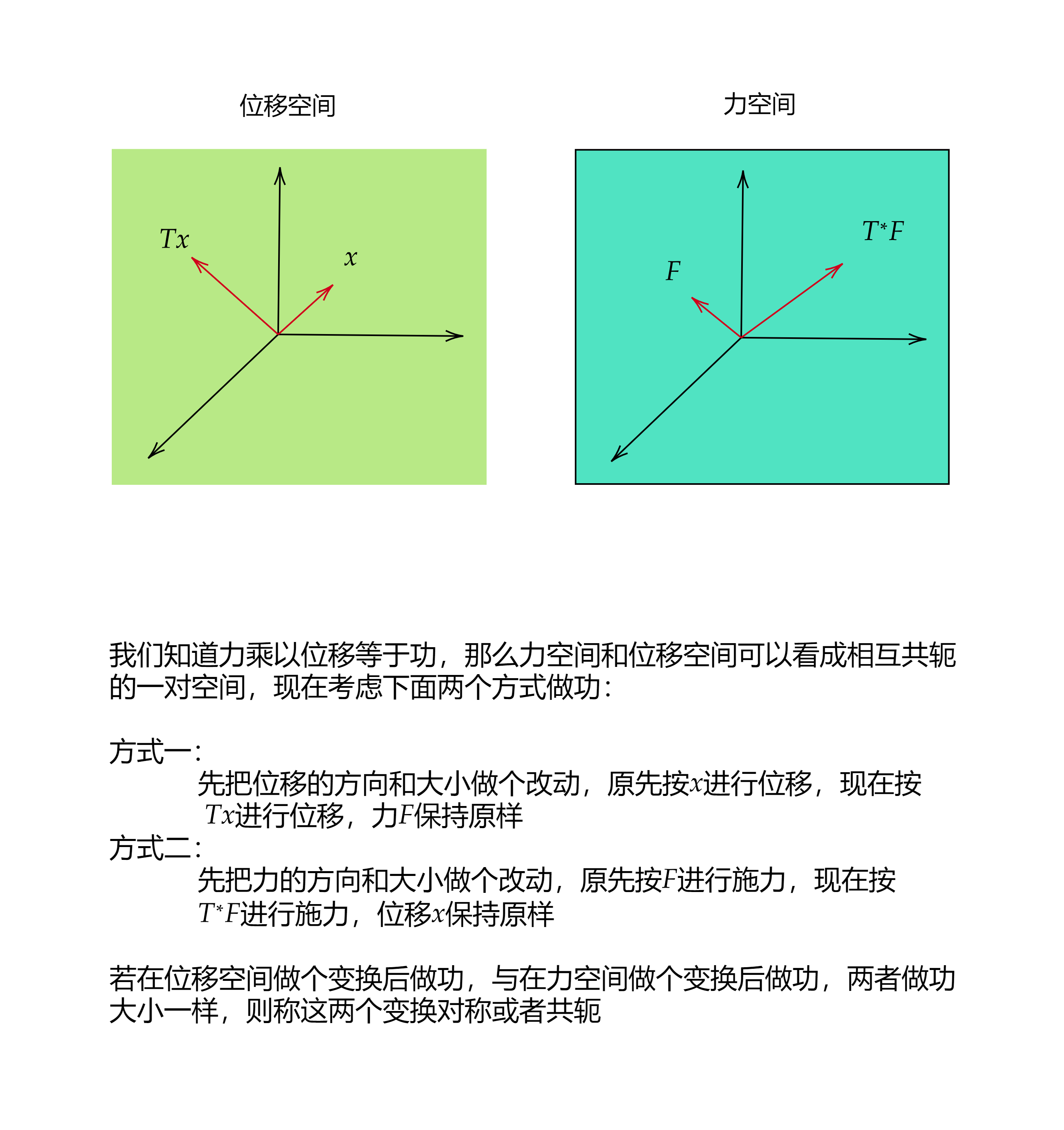
从物理角度来看
共轭算子定义的合理性
由于原始定义涉及4个空间,很复杂,这里仅讨论Hilbert空间上的共轭算子定义的合理性
(1). $T^*$ 的存在性:
取定$T,y$ , 定义 $f_{T,y}(x)=(Tx,y)$ 是H上的有界线性泛函,由Riesz表示定理,存在唯一的$z \in H,st. f_{T,y}(x) $=(x,z) ,
所以有$(Tx,y)=(x,z)$.
不妨记$z=Ay$ , 则$(Tx,y)=(x,Ay)$ , 故算子存在,但此时并不知道这是一个怎样的算子
(2). $T^*$ 的线性性:
一方面,由上面可知,$(Tx,y_1+y_2)=(x,A(y_1+y_2))$
另一方面,由内积的线性性可知,$(Tx,y_1+y_2)=(Tx,y_1)+(Tx,y_2)=(x,Ay_1)+(x,Ay_2)=(x,Ay_1+Ay_2))$
所以,$(Tx,y_1+y_2)=(x,A(y_1+y_2))=(x,Ay_1+Ay_2)$
如法炮制,容易证明$(Tx,ky)=(x,A(ky))=(x,kA(y))$
那么对于算子A有:$A(y_1+y_2)=Ay_1+Ay_2 , A(ky)=kA(y) $
A是线性算子
(3). $T^*$ 的有界性:
$\|Ay\|=\|z\| \quad \overset{Riesz表示定理}{=} \quad \|f_{T,y}\| \leq \|T\|\cdot\|y\| $
综上所述,这样的算子存在,后面记$A=T^*$
共轭算子的基本性质
设 $ A 、 B $ 是 Hilbert 空间 $ H $ 上的有界线性算子, 则
(1).$\|A^\ast\|=\|A\|, (A^\ast)^ \ast=A; $
(2). $ (A+B)^\ast=A^*+B^\ast ; $
(3). $ (A B)^\ast=B^\ast A^\ast $
(4). $ (\alpha A)^\ast=\bar{\alpha} A^\ast , \forall \alpha \in \mathbb{K} ; $
(5). $ \|A^\ast A\|=\|A A^\ast \|=\|A\|^{2}=\|A^\ast \|^{2} $
(6). 若 $ A^{-1} $ 存在且有界, 则 $(A^\ast )^{-1}$ 也存在且有界, 且$ \left(A^\ast \right)^{-1}=\left(A^{-1}\right)^\ast . $
证明:
较为简单,略
有界自共轭算子的性质
设 $ A 、 B $ 是 Hilbert 空间 $ H $ 上的有界自共轭线性算子, 则
(1). $ AB $ 自共轭 $\Leftrightarrow AB=BA ;$
(2). $ A $ 自共轭 $\Leftrightarrow (x,Ax) \text{是实的} ;$
(3). $\|A\|=\sup\limits_{\|x\|=1}(x,Ax) . $
证明:
(1)较为简单,(2)、(3)需要用到类似平行四边形法则的公式变形,纯技巧,证明略

