介绍泛函分析中的四大基本定理:一致有界原则和共鸣定理,开映射定理和逆算子定理,闭算子定理,Hahn-Banach延拓定理
第3章 泛函分析四大基本定理
设 $ X, X_{1} $ 是赋范线性空间, $ \mathscr{B}\left(X, X_{1}\right) $ 表示从 $ X $ 到 $ X_{1} $ 的全体有界线性算子.
一致有界原则
条件:
(1). $X$是Banach空间
(2). $T_{\alpha}$是有界算子族,且点点有界,即 $ \forall x \in X , \sup_\limits{\alpha \in \mathbf{I}}\|T_{\alpha}x\|\leq M_x $
结论:
$T_{\alpha}$一致有界,即 $ \sup_\limits{\alpha \in \mathbf{I}}\|T_{\alpha}\|\leq M $
证明思路:
要证明$T_{\alpha}$一致有界,只需要证明$T_{\alpha}$在一个范数球上一致有界,为此,先将X分解,$ X=\cup_{k=1}^{\infty}M_k , \quad M_{k}=\left\{x \mid\left\|T_{\alpha} x\right\| \leqslant k, \forall \alpha \in I\right\}(k=1,2, \cdots)$ ,
这样$T_{\alpha}$在每一个$M_k$上一致有界,并且由于范数的连续性,每个$M_k$是闭集(这点在后面很重要),另一方面,由于X是第二纲集,所以必定存在一个$M_{k_0}$ 不是疏集,
则$M_{k_0}$ 在一个闭球$\overline{B}$ 中稠密,即$\overline{B} \subset \overline{M_{k_0}}=M_{k_0}$
由于 $T_{\alpha}$ 在 $M_{k_0}$ 上一致有界,所以 $T_{\alpha}$ 在闭球 $\overline{B}$ 上一致有界,通过平移伸缩可以得到$T_{\alpha}$在一个范数球上一致有界
注:$M_{k_0}$ 在一个闭球$\overline{B}$ 中稠密,那么也可以通过平移伸缩证明$M_{k_0}$ 在一个以原点为中心的闭球中稠密,这样就可以直接得到 $T_{\alpha}$ 在一个以原点为中心的闭球上一致有界
逆否命题(共鸣定理):
条件:
(1). $X$是Banach空间
(2). $T_{\alpha}$是有界算子族,且 $ \sup_\limits{\alpha \in \mathbf{I}}\|T_{\alpha}\|= \infty $
结论:
$ \exists \quad x_0 \in X , \quad st.\quad \sup_\limits{\alpha \in \mathbf{I}}\|T_{\alpha}x_0\|=\infty $
开映射定理
条件:
(1). $X,X_1$都是Banach空间
(2). $T$是满射
结论:
$T$把 $X$中的开集映成 $X_1$中的开集
证明思路:
一、对于所要证明的结论这边,做个转化
(1).第一步转化
要证明 $T$把 $X$中的开集$G$映成 $X_1$中的开集$TG$, 就是说对于G中的任意一点映射过去都是内点,
即 $\forall x \in G,$ 是否存在 $ r > 0?$ 使得 $B_1(Tx,r)\subset TG$,
但这个并不好证明,先把问题进行一个转换,如下分析:
对于$\forall x \in G$,由于$x$是$G$中的内点,所以$\exists r_2>r_1 > 0,st.\overline{B}(x,r_1)\subset B(x,r_2) \subset G$,
那么就有$T \overline{B}(x,r_1)\subset TB(x,r_2) \subset TG$,
这步是为了将$TG$上的讨论转为$T \overline{B}(x,r_1)$ 上的讨论,即问题转化为:
$\forall x \in G,$ 是否存在 $ r > 0?$ 使得 $B_1(Tx,r)\subset T \overline{B}(x,r_1)$ , 其中 $ r_1 $ 是一个已知量
(2).第二步转化
注意到 $ T $ 是线性算子
$B_{1}(T x, r)=T x+B_{1}(0, r),$
$T \bar{B}\left(x, r_{1}\right)=T\left(x+\bar{B}\left(0, r_{1}\right)\right)=T x+T \bar{B}\left(0, r_{1}\right) .$
问题转化为: 是否存在 $ r>0 $, 使得
$B_{1}(0, r) \subset T \bar{B}\left(0, r_{1}\right)$ , 其中 $ r_1 $ 是一个已知量
二、挖掘已有的条件
(1). 根据结论中的集合形式,由条件向结论靠拢
考虑 $ X=\bigcup\limits_{k=1}^{\infty} \bar{B}(0, k), X_{1}=T X=\bigcup\limits_{k=1}^{\infty} T \bar{B}(0, k) . $
由于 $ X_ {1} $ 是 $ Banach $ 空间, 由 $ Baire $ 纲定理知, $ X_{1} $ 是第二纲集, 于是存在 $ k_{0} $ , $ T \bar{B}\left(0, k_{0}\right) $ 不是疏集.
所以 $ T \bar{B}\left(0, k_{0}\right) $ 在某个小球 $ B_{1}\left(y_{0}, r_{0}\right) $ 中稠密, 即
$ B_{1}\left(y_{0}, r_{0}\right) \subset \overline{T \bar{B}\left(0, k_{0}\right)} . $
通过平移压缩可以进一步得到
$ T \bar{B}\left(0, k_{0}\right) $ 在小球 $ B_{1}\left(0, r_{0}\right) $ 中稠密, 即
$ B_{1}\left(0, r_{0}\right) \subset \overline{T \bar{B}\left(0, k_{0}\right)} $ , 其中$k_0$已知,$r_0$是根据$k_0$找到的
(2). 试着由条件向结论推,发现问题所在
如果直接利用上述条件向结论推,我们会得到(先忽略$k_0$是整数,$r_1$不一定是整数这点):
给了$ r_1 $后,根据条件,我们可以找到$ r $,使得 $ B_{1}\left(0, r\right) \subset \overline{T \bar{B}\left(0, r_{1}\right)} $ ,
这并不是所要证明的结论,右边的集合多了个闭包
(3). 为了解决问题,先给个过渡引理
若$A \subset \bar{B}$,则 $\forall \varepsilon >0 ,a \in A $, 则 $a \in \bar{B}$,那么 $\exists b \in B , st. |b-a|<\varepsilon$
通俗来说就是,A中的任一元素,虽然不一定在B中,但可以在B中找到一个元素逼近它
(4). 再一次观察条件,设法给出构造性证明
从上面条件能推理到的地方出发
$ B_{1}\left(0, r\right) \subset \overline{T \bar{B}\left(0, r_{1}\right)} $ ,对于 $\forall y \in B_{1}\left(0, r\right) $ , 我们可以在 $T \bar{B}\left(0, r_{1}\right)$ 中找到一个元素 $Ts_1$ 逼近 $y$ (其中 $s_1 \in \bar{B}(0, r_{1}) $),
这只能说明$y$离 $T \bar{B}\left(0, r_{1}\right)$ 很近,不能说明$y$就在 $T \bar{B}\left(0, r_{1}\right)$ 里头
假设我们找到了一列元素 $Ts_n$ 逼近 $y$ ,即 $\lim\limits_{n \rightarrow \infty} Ts_n=Ts=y$ , 并且还有 $s \in \bar{B}(0, r_{1}) $ , 这就说明 $Ts \in T \bar{B}\left(0, r_{1}\right)$ , 也就是 $y \in T \bar{B}\left(0, r_{1}\right)$
注:上面序列取完极限后,是否还在原来的集合里很重要,$s \in \bar{B}(0, r_{1}) $ 这步是关键
(5). 下方给出构造性证明,因为是构造性证明,不要问为什么这么构造
接着从$ B_{1}\left(0, r\right) \subset \overline{T \bar{B}\left(0, r_{1}\right)} $ 出发,这句话意思给定一个$r_1$就有一个$r$使得这个包含关系式成立,
令$\delta = r/r_1$,通过伸缩得到$ B_{1}\left(0, \delta\right) \subset \overline{T \bar{B}\left(0, 1\right)} $ , 从这个式子出发,通过伸缩得到下面一列关系式:
$ B_{1}\left(0, \delta/2\right) \subset \overline{T \bar{B}\left(0, 1/2\right)} $
$ B_{1}\left(0, \delta/2^2\right) \subset \overline{T \bar{B}\left(0, 1/2^2\right)} $
$ B_{1}\left(0, \delta/2^3\right) \subset \overline{T \bar{B}\left(0, 1/2^3\right)} $
……
$ B_{1}\left(0, \delta/2^n\right) \subset \overline{T \bar{B}\left(0, 1/2^n\right)} $
下面每一步都是根据过渡引理和上面的每一个关系式得到的:
i.对于 $\varepsilon=\delta/2^2 , \forall y \in B_{1}\left(0, \delta/2\right) , \exists Tx_1 \in T \bar{B}\left(0, 1/2\right) st.\|y-Tx_1\|<\delta/2^2 $ ,
可以得到$y-Tx_1 \in B_{1}\left(0, \delta/2^2\right)$
ii. 对于$\varepsilon=\delta/2^3 , y-Tx_1 \in B_{1}\left(0, \delta/2^2\right) , \exists Tx_2 \in T \bar{B}\left(0, 1/2^2\right) st.\|y-Tx_1-Tx_2\|<\delta/2^3 $ ,
可以得到 $y-Tx_1-Tx_2 \in B_{1}\left(0, \delta/2^3\right)$
……
依次做下去,可以得到
$y-Tx_1-Tx_2-\dots-Tx_n \in B_{1}\left(0, \delta/2^{n+1}\right)$ 且 $ x_n \in \bar{B}\left(0, 1/2^n\right) $
一方面,令$s_n=\sum\limits_{k=1}^{n}x_k$ , 则 $s_n \in \bar{B}(0, 1/2^n)$ , 由于$\|x_k\| \leq 1/2^k$ , 所以$ \{s_n\} $ 收敛,
设$\lim\limits_{n \to \infty}s_n=s$ , 则有$\|s\|\leq \sum\limits_{k=1}^{\infty}\|x_k\| \leq 1$ , 那么有$s \in \bar{B}(0,1),Ts \in T \bar{B}(0,1)$ .
另一方面,$\|y-Tx_1-Tx_2-\dots-Tx_n\|=\|y-s_n\| \leq \delta/2^{n+1}$ , 令$n \to \infty$ ,
得到$y=\lim\limits_{n \to \infty}Ts_n=Ts\in T \bar{B}(0,1)$
综上,得到如下结果:
$\forall y \in B_{1}\left(0, \delta/2\right) , $ 有 $y \in T \bar{B}(0,1)$ , 即$ B_{1}\left(0, \delta/2\right) \subset T \bar{B}\left(0, 1/2\right) $
把 $\delta $ 换回 $ r/r_1$ , 并简单伸缩,得到 $ B_{1}\left(0, r\right) \subset T \bar{B}\left(0, r_{1}\right) $ ,这正是结论所要证明的关系式。
逆算子定理
条件:
(1). $X,X_1$都是Banach空间
(2). $T$是双射
结论:
$T^{-1}$有界
证明:
设 $G \subset X , G_1 \subset X_1, T^{-1}(G_1)=G, $
若 $G$ 是开集,由开映射定理可知,$T(G)$是开集 , 而$T(G)=T T^{-1}(G_1)=G_1$ ,
说明对于$T^{-1}$ , 开集的原像是开集,$T^{-1}$连续,即$T^{-1}$有界
另一个与逆算子有关的定理
$ T$ 是赋范空间 $ X$ 中到赋范空间 $ X_{1}$ 中的线性算子, 如果存在 $ m>0$ , 使得
$\|T x\| \geqslant m\|x\| \quad(x \in \mathscr{D}(T)),$ 则 $ T$ 存在有界的逆算子 $ T^{-1} .$ 反之,如果
$R(T)$上的逆算子$T^{-1}$存在且有界,则上式成立.
证明:
“$\Rightarrow $”
(1) 证 $ T $ 是一对一的. 如果 $T x_{1}=T x_{2} $ , 则 $T\left(x_{1}-x_{2}\right)=0 $ , 但
$\left\|T\left(x_{1}-x_{2}\right)\right\| \geqslant m\left\|x_{1}-x_{2}\right\|, $
因此, $ \left\|x_{1}-x_{2}\right\|=0 $, 即 $ x_{1}=x_{2} $ . 故 $ T $ 是一对一的, 于是逆算子 $ T^{-1}: \mathscr{R}(T) \rightarrow \mathscr{D}(T) $ 存在.
(2) 证 $T^{-1} $ 是有界的. 对于任意的 $ y \in \mathscr{R}(T), T^{-1} y \in \mathscr{D}(T) $. 由条件
$\left\|T\left(T^{-1} y\right)\right\| \geqslant m\left\|T^{-1} y\right\|, $
即 $ \|y\| \geqslant m\left\|T^{-1} y\right\| $, 于是我们有
$\left\|T^{-1} y\right\| \leqslant \frac{1}{m}\|y\|, \forall y \in \mathscr{R}(T), $
$ T^{-1} $ 是有界线性算子.
“$\Leftarrow$”
反之, 如果定义在 $ \mathscr{R}(T) $ 上的逆算子 $ T^{-1} $存在且有界, 但结论不成立, 则对每个正整数 $n $ , 存在 $ x_{n} \in \mathscr{D}(T) $, 使得
$\left\|T x_{n}\right\|<\frac{1}{n}\left\|x_{n}\right\| \text {. } $
设 $ y_{n}=T x_{n}, x_{n}=T^{-1} y_{n} $, 则
$n\left\|y_{n}\right\|<\left\|T^{-1} y_{n}\right\|, $
由此推出 $ T^{-1} $ 无界, 矛盾.
闭算子定理
乘积空间:
$X \times X_1 = \{ (x,y): x \in X, y \in X_1 \}$
乘积空间中的范数定义:
$\|(x,y)\|=\|x\|+\|y\|$
算子T的图像:
$G(T)=\{(x,Tx): x \in D(T)\}$
闭算子定义:
$G(T)$是闭集,则称算子$T$是闭的
闭算子定理:
$T$是闭算子 “$ \Leftrightarrow $” $\forall x_n \to x , y_n \to y ,\text{有} x \in D(T) , y=Tx$
证明:
充分性.
由定理的条件成立, 证 $ G(T) $ 是闭的, 即证明 $ \forall(x, y) \in \overline{G(T)} \Rightarrow (x, y) \in G(T) .
\forall(x, y) \in \overline{G(T)} , $ 存在 $ \left(x_{n}, y_{n}\right) \in G(T) , $ 使得
$ \left(x_{n}, y_{n}\right) \rightarrow(x, y)(n \rightarrow \infty) . $
因 $ \left(x_{n}, y_{n}\right) $ 在 $ T $ 的图像中, 故 $ y_{n}=T x_{n} , $ 即
$ \left(x_{n}, T x_{n}\right) \in G(T),\left(x_{n}, T x_{n}\right) \rightarrow(x, y)(n \rightarrow \infty) . $
根据乘积空间范数的定义有
$ \left\|x_{n}-x\right\|+\left\|T x_{n}-y\right\| \rightarrow 0(n \rightarrow \infty) . $
所以
$ \left\|x_{n}-x\right\| \rightarrow 0,\left\|T x_{n}-y\right\| \rightarrow 0(n \rightarrow \infty), $
即
$ x_{n} \rightarrow x, \quad T x_{n} \rightarrow y . $
由定理中的条件可知
$ x \in \mathscr{D}(T), y=T x . $
故 $ (x, y) \in G(T) , $ 这就证明了 $ T $ 是闭算子.
必要性.
已知 $ T $ 是闭的, 要证明定理中的条件成立. 即证明 $ \forall\left\{x_{n}\right\} \subset \mathscr{D}(T), x_{n} \rightarrow x, T x_{n} \rightarrow y(n \rightarrow \infty) , $ 则有 $ x \in \mathscr{D}(T), y=T x . $
由条件有
$ \left\|x_{n}-x\right\|+\left\|T x_{n}-y\right\| \rightarrow 0(n \rightarrow \infty), $
因而
$ \left(x_{n}, T x_{n}\right) \rightarrow(x, y) . $
因为 $ T $ 是闭的, 即 $ G(T) $ 是闭的, 故 $ (x, y) \in G(T) , $ 即
$ x \in \mathscr{D}(T), \quad y=T x . $
Hahn-Banach定理
设$f$是定义在赋范线性空间$X$的子集$G$上的有界线性泛函,则$f$可以保范延拓至全空间$X$上
证明思路:
先将$f$从$G$上保范延拓至G和G外一点$x_1$张成的子空间上,再由Zorn引理(差不多就是数学归纳法用在不可数的情况)即可得到结论
这里证明过程不再给出,一般泛函书籍都有介绍,下面给出这个延拓的几何直观解释
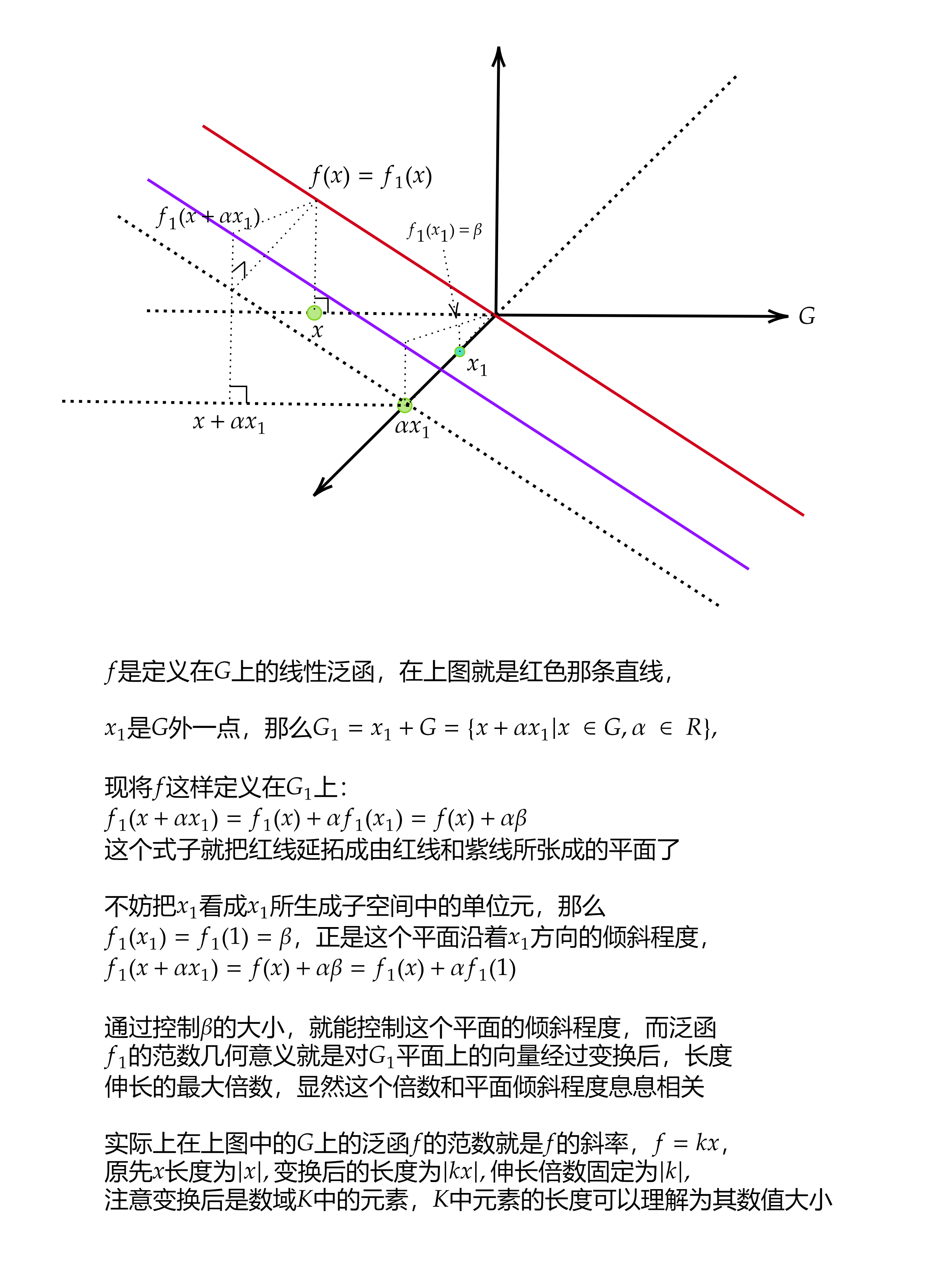
线性泛函和闭集分离定理
设 $ G $ 是赋范空间$ X$ 的子空间, $ x_{1} \in X ,$ 如果
$ d=d\left(x_{1}, G\right)=\inf\limits _{x \in G}\left\|x-x_{1}\right\|>0,$
则存在 $ X $ 上的有界线性泛函 $ f_1 ,$
$ \|f_1\|=\frac{1}{d} ; \quad f_1\left(x_{1}\right)=1 ; f_1(x)=0, \forall x \in G $
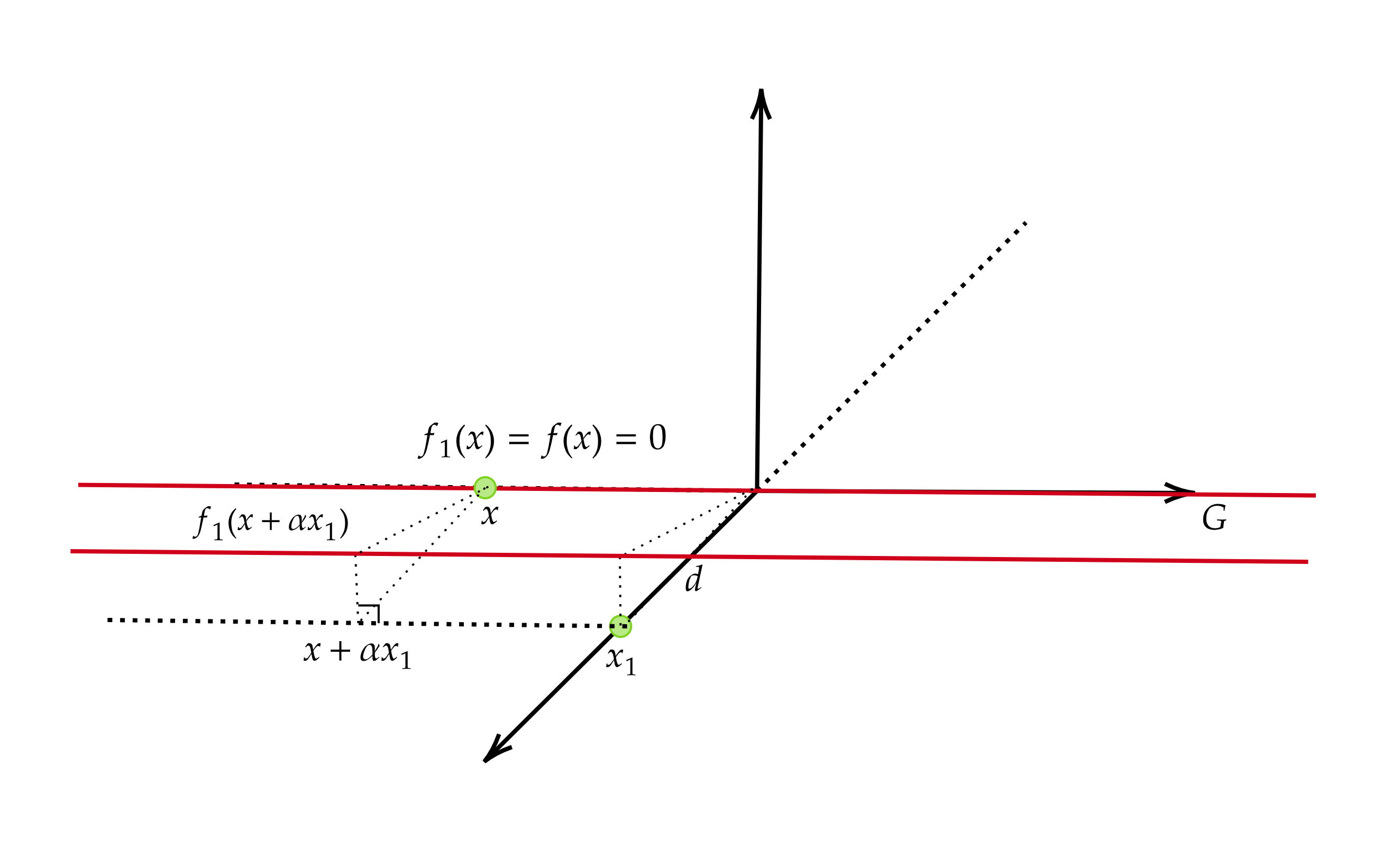
注:闭集分离定理和延拓定理本质是一回事,两者可以相互推,关于这个定理在连续函数中也有类似结论,参考Tietze扩张

